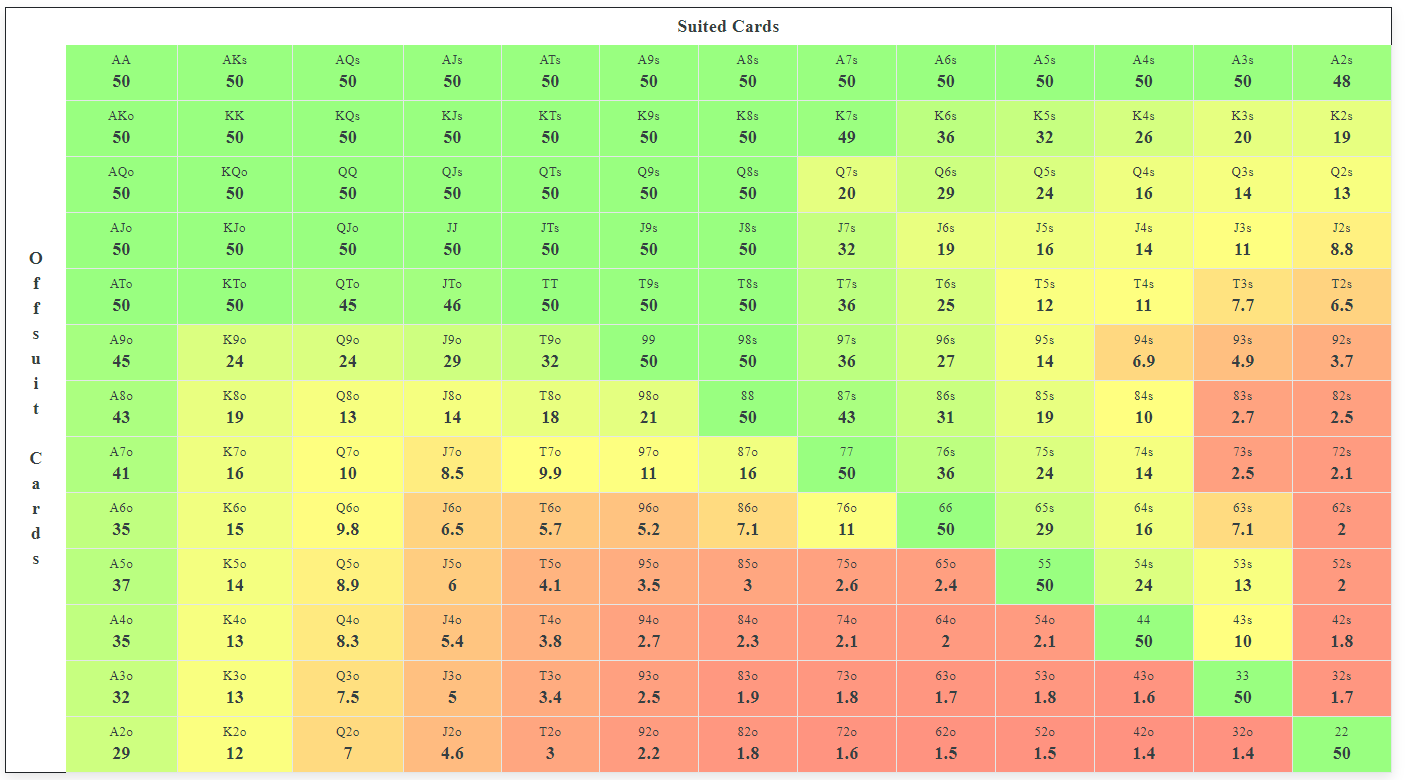
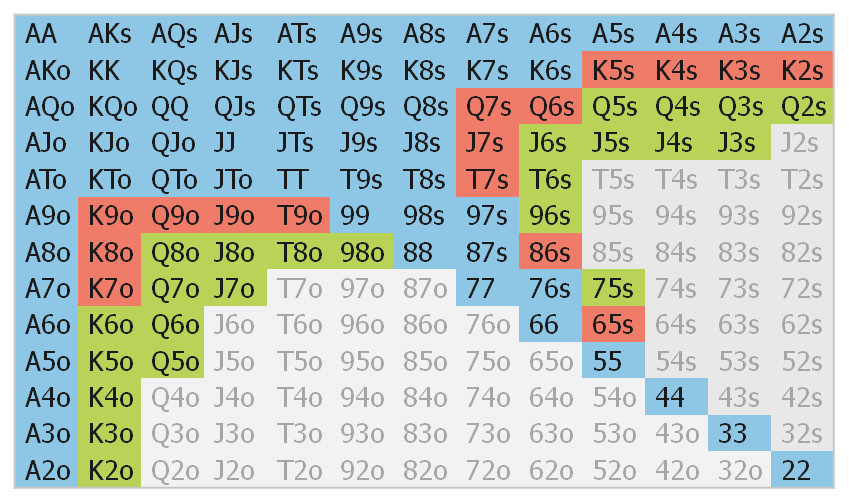
- Push Fold Chart Poker
- Nash Poker Chart
- Tableau De Nash Poker
- Nash Equilibrium Poker
- Live Poker Cash Games
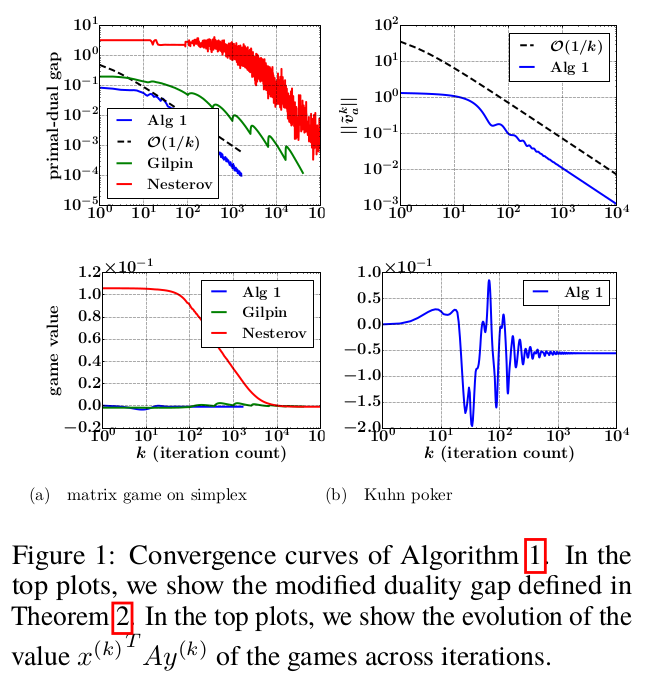
Kuhn poker is an extremely simplified form of poker developed by Harold W. Kuhn as a simple model zero-sum two-player imperfect-information game, amenable to a complete game-theoretic analysis. In Kuhn poker, the deck includes only three playing cards, for example a King, Queen, and Jack. One card is dealt to each player, which may place bets similarly to a standard poker. If both players bet or both players pass, the player with the higher card wins, otherwise, the betting player wins.
Game description[edit]
'Nash Bridges' Liar's Poker (TV Episode 2000) cast and crew credits, including actors, actresses, directors, writers and more. If you think about it, that means that every poker situation and poker in general has its own Nash equilibrium. In theory, if everyone plays perfectly, even no-limit hold'em is a solved game. Should we start panicking? First of all, there is a huge difference between knowing there is a Nash equilibrium and finding one. ICMIZER is a time-tested favorite Nash calculator of thousands of poker players worldwide. Utilizing poker ICM theory, cutting edge FGS model, and a basic ChipEV model, it offers a wide range of tools for optimizing your preflop Push/Fold playing strategy. Nash clay poker set Thanks to a double injection, iron core, and a weight of 14 grams,every detail of the NASH clay chips has been crafted with the upmost attention to.
In conventional poker terms, a game of Kuhn poker proceeds as follows:
Push Fold Chart Poker
Nash equilibrium applied to poker should therefore allow a player never to lose, whatever the opponent's strategy. Consequently, there are no regrets to be had in case of defeat since one played in the best possible manner; the one that ensures long-term profit.
- Each player antes 1.
- Each player is dealt one of the three cards, and the third is put aside unseen.
- Player one can check or bet 1.
- If player one checks then player two can check or bet 1.
- If player two checks there is a showdown for the pot of 2 (i.e. the higher card wins 1 from the other player).
- If player two bets then player one can fold or call.
- If player one folds then player two takes the pot of 3 (i.e. winning 1 from player 1).
- If player one calls there is a showdown for the pot of 4 (i.e. the higher card wins 2 from the other player).
- If player one bets then player two can fold or call.
- If player two folds then player one takes the pot of 3 (i.e. winning 1 from player 2).
- If player two calls there is a showdown for the pot of 4 (i.e. the higher card wins 2 from the other player).
- If player one checks then player two can check or bet 1.
Optimal strategy[edit]
The game has a mixed-strategyNash equilibrium; when both players play equilibrium strategies, the first player should expect to lose at a rate of −1/18 per hand (as the game is zero-sum, the second player should expect to win at a rate of +1/18). There is no pure-strategy equilibrium.
Kuhn demonstrated there are infinitely many equilibrium strategies for the first player, forming a continuum governed by a single parameter. In one possible formulation, player one freely chooses the probabilityα∈[0,1/3]{displaystyle alpha in [0,1/3]} with which he will bet when having a Jack (otherwise he checks; if the other player bets, he should always fold). When having a King, he should bet with the probability of 3α{displaystyle 3alpha } (otherwise he checks; if the other player bets, he should always call). He should always check when having a Queen, and if the other player bets after this check, he should call with the probability of α+1/3{displaystyle alpha +1/3}.
The second player has a single equilibrium strategy: Always betting or calling when having a King; when having a Queen, checking if possible, otherwise calling with the probability of 1/3; when having a Jack, never calling and betting with the probability of 1/3.
Generalized versions[edit]
In addition to the basic version invented by Kuhn, other versions appeared adding bigger deck, more players, betting rounds, etc., increasing the complexity of the game.
3-player Kuhn Poker[edit]
A variant for three players was introduced in 2010 by Nick Abou Risk and Duane Szafron. In this version, the deck includes four cards (adding a ten card), from which three are dealt to the players; otherwise, the basic structure is the same: while there is no outstanding bet, a player can check or bet, with an outstanding bet, a player can call or fold. If all players checked or at least one player called, the game proceeds to showdown, otherwise, the betting player wins.
A family of Nash equilibria for 3-player Kuhn poker is known analytically, which makes it the largest game with more than two players with analytic solution.[1] The family is parameterized using 4–6 parameters (depending on the chosen equilibrium). In all equilibria, player 1 has a fixed strategy, and he always checks as the first action; player 2's utility is constant, equal to –1/48 per hand. The discovered equilibrium profiles show an interesting feature: by adjusting a strategy parameter β{displaystyle beta } (between 0 and 1), player 2 can freely shift utility between the other two players while still remaining in equilibrium; player 1's utility is equal to −1+2β48{displaystyle -{frac {1+2beta }{48}}} (which is always worse than player 2's utility), player 3's utility is 1+β24{displaystyle {frac {1+beta }{24}}}.
It is not known if this equilibrium family covers all Nash equilibria for the game.
References[edit]
- Kuhn, H. W. (1950). 'Simplified Two-Person Poker'. In Kuhn, H. W.; Tucker, A. W. (eds.). Contributions to the Theory of Games. 1. Princeton University Press. pp. 97–103.
- James Peck. 'Perfect Bayesian Equilibrium'(PDF). Ohio State University. Retrieved 2 September 2016.:19–29
- ^Szafron, Duane; Gibson, Richard; Sturtevant, Nathan (May 2013). 'A Parameterized Family of Equilibrium Profiles forThree-Player Kuhn Poker'(PDF). In Ito; Jonker; Gini; Shehory (eds.). Proceedings of the 12th International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2013). Saint Paul, Minnesota, USA.
External links[edit]
A two-page paper published by John Nash in 1950 is a seminal contribution to the field of Game Theory and of our general understanding of strategic decision-making. That paper, 'Equilibrium points in N-person games', introduced a cornerstone concept which came to be known as Nash equilibrium.
Game theory is concerned with situations where decisions interact – where the 'payoff' or reward for a decision maker depends not only on his or her own decision but also on the decisions of others.
Such situations are pervasive in real life. The payoff for a buyer in an auction, for example, depends not only on the amount he bids but also on the bids of the other buyers. If the buyer's bid is not the highest, then he loses the auction. Likewise, the profit realised by a firm depends not only on the price it sets for its product but also on the prices set by its competitors. In a tennis match, the likelihood the server will win a point depends on whether she delivers the serve to the receiver's left or right and whether the receiver correctly anticipates it.
Auctions, price setting and tennis are all examples of 'non-cooperative' strategic interactions that mathematicians and economists refer to as 'games'. They are non-cooperative because decision makers take their actions independently and are unable to enter into binding agreements with others regarding their actions, either because such agreements are illegal (when setting prices) or because they have no incentive to do so (as in tennis).
The notion of Nash equilibrium, developed in Nash's 1950 paper, is the basis of how economists predict the outcome of strategic interactions.
Informally, a Nash equilibrium is a list of actions, one for each decision maker, such that each decision maker's action is best for him, given the actions of the others. Such a list of actions is an equilibrium (or stable point), since no decision maker has an incentive to change his action.

Consider a driver approaching an intersection. She stops when she approaches a red light and she continues without concern when she approaches a green light. It is a Nash equilibrium when all drivers behave this way. When approaching a red light it is best to stop since the crossing traffic has a green light and will continue. When approaching a green light it is best to continue since the crossing traffic has a red light and will stop. Thus it is in each driver's own interest to play her part in the equilibrium, given that everyone else does. No traffic cop is required.
Nash equilibrium also allows for the possibility that decision makers follow randomised strategies. Allowing for randomisation is important for the mathematics of game theory because it guarantees that every (finite) game has a Nash equilibrium.
Randomisation is also important in practice in commonly played games such as Two-up, Rock-Paper-Scissors, poker and tennis. We all know from our own experience how to play Rock-Paper-Scissors against a sophisticated opponent: play each action with equal probability, independently of the actions and outcomes in past plays. Indeed, this is exactly what Nash equilibrium predicts. Nash's theory applies to any game with any number of decision makers, whereas John von Neumann's 1928 Minimax Theorem applies only to 'zero-sum' games with two players.
Interestingly, data collected from championship tennis matches has shown that the serve-and-return behaviour of professional players is consistent with both von Neumann's Minimax Theory and Nash's generalisation.
Nash's work dealt with games in which each decision maker takes his or her action without knowing the actions taken by others, and in which no decision-maker has private information. John Harsanyi extended the notion of Nash equilibrium to deal with strategic interactions, such as in auctions, in which decision-makers have private information. (In an auction, buyers know the value they place on the item being sold, but they don't know how other buyers value the item.)
Nash Poker Chart
Reinhardt Selten extended the notion of Nash equilibrium to deal with dynamic interactions, in which one or more decision-makers observe the action of another before taking their own action. In 1994, Nash shared the Nobel Prize in Economics with Harsanyi and Selten for these contributions.
Tableau De Nash Poker
While Nash is best known for his contribution to non-cooperative game theory, he also made a seminal contribution to cooperative game theory with the development of the Nash bargaining solution.
Nash's work has had a profound impact in economics. Knowledge of game theory is essential training for every professional economist and it is a common – and popular – subject for undergraduate students as well. Nash's work not only revolutionised modern economics, it has also had an important impact in fields as diverse as computer science, political science, sociology and biology.
His work on game theory won him a Nobel Prize for economics in 1994 and he just recently received Norway's Abel prize for mathematics.
A two-page paper published by John Nash in 1950 is a seminal contribution to the field of Game Theory and of our general understanding of strategic decision-making. That paper, 'Equilibrium points in N-person games', introduced a cornerstone concept which came to be known as Nash equilibrium.
Game theory is concerned with situations where decisions interact – where the 'payoff' or reward for a decision maker depends not only on his or her own decision but also on the decisions of others.
Such situations are pervasive in real life. The payoff for a buyer in an auction, for example, depends not only on the amount he bids but also on the bids of the other buyers. If the buyer's bid is not the highest, then he loses the auction. Likewise, the profit realised by a firm depends not only on the price it sets for its product but also on the prices set by its competitors. In a tennis match, the likelihood the server will win a point depends on whether she delivers the serve to the receiver's left or right and whether the receiver correctly anticipates it.
Auctions, price setting and tennis are all examples of 'non-cooperative' strategic interactions that mathematicians and economists refer to as 'games'. They are non-cooperative because decision makers take their actions independently and are unable to enter into binding agreements with others regarding their actions, either because such agreements are illegal (when setting prices) or because they have no incentive to do so (as in tennis).
The notion of Nash equilibrium, developed in Nash's 1950 paper, is the basis of how economists predict the outcome of strategic interactions.
Informally, a Nash equilibrium is a list of actions, one for each decision maker, such that each decision maker's action is best for him, given the actions of the others. Such a list of actions is an equilibrium (or stable point), since no decision maker has an incentive to change his action.
Consider a driver approaching an intersection. She stops when she approaches a red light and she continues without concern when she approaches a green light. It is a Nash equilibrium when all drivers behave this way. When approaching a red light it is best to stop since the crossing traffic has a green light and will continue. When approaching a green light it is best to continue since the crossing traffic has a red light and will stop. Thus it is in each driver's own interest to play her part in the equilibrium, given that everyone else does. No traffic cop is required.
Nash equilibrium also allows for the possibility that decision makers follow randomised strategies. Allowing for randomisation is important for the mathematics of game theory because it guarantees that every (finite) game has a Nash equilibrium.
Randomisation is also important in practice in commonly played games such as Two-up, Rock-Paper-Scissors, poker and tennis. We all know from our own experience how to play Rock-Paper-Scissors against a sophisticated opponent: play each action with equal probability, independently of the actions and outcomes in past plays. Indeed, this is exactly what Nash equilibrium predicts. Nash's theory applies to any game with any number of decision makers, whereas John von Neumann's 1928 Minimax Theorem applies only to 'zero-sum' games with two players.
Interestingly, data collected from championship tennis matches has shown that the serve-and-return behaviour of professional players is consistent with both von Neumann's Minimax Theory and Nash's generalisation.
Nash's work dealt with games in which each decision maker takes his or her action without knowing the actions taken by others, and in which no decision-maker has private information. John Harsanyi extended the notion of Nash equilibrium to deal with strategic interactions, such as in auctions, in which decision-makers have private information. (In an auction, buyers know the value they place on the item being sold, but they don't know how other buyers value the item.)
Nash Poker Chart
Reinhardt Selten extended the notion of Nash equilibrium to deal with dynamic interactions, in which one or more decision-makers observe the action of another before taking their own action. In 1994, Nash shared the Nobel Prize in Economics with Harsanyi and Selten for these contributions.
Tableau De Nash Poker
While Nash is best known for his contribution to non-cooperative game theory, he also made a seminal contribution to cooperative game theory with the development of the Nash bargaining solution.
Nash's work has had a profound impact in economics. Knowledge of game theory is essential training for every professional economist and it is a common – and popular – subject for undergraduate students as well. Nash's work not only revolutionised modern economics, it has also had an important impact in fields as diverse as computer science, political science, sociology and biology.
His work on game theory won him a Nobel Prize for economics in 1994 and he just recently received Norway's Abel prize for mathematics.
Nash Equilibrium Poker
John Nash remained active at scientific conferences around the world. He was happy to talk with students, many of whom wanted a picture with him too. He and his wife, Alicia were both killed in a car accident on the New Jersey Turnpike on Saturday, May 24 on their way home from receiving the prize.
Live Poker Cash Games
Both were kind people and they will be missed.

